Принципы построения трехмерной сцены
В трехмерной графике пространственные объекты, заданные в непрерывном виде, как правило, аппроксимируют (приближают) множеством треугольников. Именно треугольник представляет собой элементарный примитив, с помощью которого описываются все элементы сцены, в том числе и те, которые имеют гладкую форму (сфера, цилиндр, параметрические поверхности и др.).
Процесс формирования изображения должен учитывать две главные сущности. Это визуализируемый объект сцены и наблюдатель. Объект существует в пространстве независимо от кого-либо. Наблюдатель же представляет собой средство формирования изображения наблюдаемых объектов. Именно наблюдатель формирует изображение. Наблюдатель и наблюдаемый объект существуют в одном и том же трехмерном мире, а создаваемое при этом изображение получается двухмерным. Суть процесса формирования изображения состоит в том, чтобы, зная положение наблюдателя и положение объекта, описать (синтезировать) получаемое при этом двухмерное изображение (проекцию).
В большинстве графических библиотек присутствуют следующие сущности трехмерной сцены:
- объекты;
- наблюдатель (камера);
- источники света;
- свойства материалов объекта.
При этом моделируемая трехмерная сцена может описываться тысячами, а иногда миллионами вершин. Для каждой вершины (точки) примитива должны выполняться вычисления по одним и тем же формулам.
Как мы знаем, точка в 3D графике задается, как правило, набором из 4-х значений (x,y,z,w). Реальные координаты точки в пространстве будут (x/w, y/w, z/w), компонент w является масштабом. Обычно для точек w=1. Вектор – направленный отрезок. Вектора равны если у них одинаковая длина и направление. Вектора также задаются в виде линейного массива 1х4 (x,y,z,w), но компонент w у векторов равен 0. Для выполнения преобразований с вершинами используют матричный подход. Матрица размерности MxN – прямоугольная таблица, имеющая M строк, N столбцов и заполненная элементами одного типа. В 3D графике используют, как правило, матрицы размерности 4х4. Таким образом преобразование точки в пространстве сводится к умножению вектор-строки размерности 4 на матрицу преобразования размером 4х4:

Так, например, умножение всех вершин объекта на одну из матриц вращения приведет к вращению этого объекта вокруг оси Ox, Oy или Oz соответственно. Для сложного трансформации объекта можно использовать последовательные преобразования, которые выражаются в перемножении (конкатенации) соответствующих матриц элементарных преобразований. Таким образом, можно сначала рассчитать единую (общую) матрицу преобразования (перемножить между собой все элементарные матрицы трансформации), а затем использовать только ее. Так, например, вращение объекта вокруг совей оси и одновременное движение по кругу определенного радиуса, может быть описано следующей последовательностью матриц: Vi *MatRot1(…)*MatTrans(…)*MatRot2(…), где Vi – координаты вершин объекта, MatRot1 – матрица поворота вокруг совей оси, MatTrans – матрица перемещения, MatRot2 – матрица вращения по кругу.
Вам не придется самостоятельно запоминать и вычислять все матрицы преобразования "вручную", т.к. во всех библиотеках 3D графики они предусмотрены. В библиотеке Direct3D определен матричный тип D3DXMATRIX – это структура, которая содержит 4х4 элементов.
Элемент матрицы с индексами ij указывает на значение, хранящееся в строке с номером i и столбце с номером j. Например, элемент _32 указывает на значение m[3][2]. Обращаться к элементам матрицы (читать, записывать) можно двумя способами.
| C++ | D3DXMATRIX m; m._11 = …; или m.m[1][1] = …; |
| Pascal | var m: TD3DXMatrix; … m._11 := …; или m.m[1,1] = …; |
| C++ | D3DXMATRIX m; // Создание единичной матрицы D3DXMatrixIdentity(&m); // Создание матрицы перемещения D3DXMatrixTranslation(&m, dx, dy, dz); // Создание матрицы масштабирования D3DXMatrixScaling(&m, kx, ky, kz); // Создание матриц вращения D3DXMatrixRotationX(&m, angleX); D3DXMatrixRotationY(&m, angleY); D3DXMatrixRotationZ(&m, angleZ); |
| Pascal | var m: TD3DXMatrix; // Создание единичной матрицы D3DXMatrixIdentity(m); // Создание матрицы перемещения D3DXMatrixTranslation(m, dx, dy, dz); // Создание матрицы масштабирования D3DXMatrixScaling(m, kx, ky, kz); // Создание матриц вращения D3DXMatrixRotationX(m, angleX); D3DXMatrixRotationY(m, angleY); D3DXMatrixRotationZ(m, angleZ); |
При работе с матрицами следует учитывать, что преобразования масштабирования и вращения производятся относительно начала координат. Для комбинирования (умножения) двух матриц существует функция D3DXMatrixMultiply(), которая помещает результат перемножения двух матриц, которые передаются в качестве второго и третьего аргументов, в первый. К примеру, мы хотим повернуть объект вокруг оси Oy на угол 30 градусов и переместить его на вектор (1,2,3). Для этого можно воспользоваться правилом композиции двух элементарных преобразований с помощью матрицы поворота и матрицы перемещения.
| C++ | D3DXMATRIX matRotY, matTrans, matRes; D3DXMatrixRotationY( &matRotY, 30*D3DX_PI/180 ); D3DXMatrixTranslation( &matTrans, 1, 2, 3 ); D3DXMatrixMultiply(&matRes, &matRotY, &matTrans); |
| Pascal | var matRotY, matTrans, matRes: TD3XDMatrix; D3DXMatrixRotationY( matRotY, 30*pi/180 ); D3DXMatrixTranslation( matTrans, 1, 2, 3 ); D3DXMatrixMultiply( matRes, matRotY, matTrans ); |
| C++ | D3DXMATRIX matRotY, matTrans; D3DXMatrixRotationY( &matRotY, … ); D3DXMatrixTranslation( &matTrans, … ); device->SetTransform(D3DTS_VIEW, D3DXMatrixMultiply(NULL, &matRotY, &matTrans)); |
| Pascal | var matRotY, matTrans, matRes: TD3XDMatrix; D3DXMatrixRotationY( matRotY, … ); D3DXMatrixTranslation( matTrans, … ); device.SetTransform(D3DTS_VIEW, D3DXMatrixMultiply(nil, matRotY, matTrans)^); |
- Моделируемые объекты трехмерного мира (сцены);
- Положение виртуальной камеры, которая определяет перспективу.
В терминах систем координат процесс получения проекции может быть описан следующей упрощенной блок схемой:
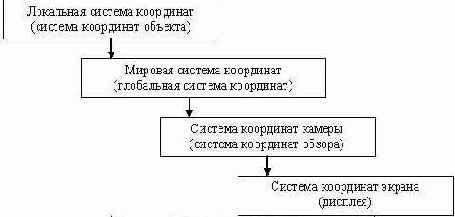
Как известно из курса линейной алгебры, переход от одной системы координат к другой эквивалентен смене базиса. Когда нужно преобразовать объект из одного базиса в другой, нужно умножить все вершины объекта на соответствующую матрицу приведения базиса.
Библиотека Direct3D позволяет работать как в левосторонней системе координат, так и в правосторонней. Далее будем рассматривать все примеры для левосторонней системы координат.
Локальная система координат (локальное пространство) определяет исходные координаты объекта, т.е. в тех в которых он задан. Моделирование объекта в локальной (собственной) системе координат удобнее, чем напрямую в мировой системе координат. Локальная система позволяет описывать объект, не обращая внимания на положение, размер, ориентацию других объектов в мировой системе координат.
После того как заданы все объекты в своих собственных (локальных) системах координат, необходимо привязать их к общей мировой системе координат. Процесс трансформации координат объектов, заданных в локальных системах в мировую (общую) называют мировым преобразованием (world transform). Обычно используют 3 типа преобразований: перемещение, масштабирование, вращение. Мировое преобразование описывается с помощью матрицы, используя метод SetTransform интерфейса IDirect3DDevice9. Для применения мирового преобразования метод SetTransform вызывается с параметром D3DTS_WORLD. Предположим, что у нас в сцене присутствуют два объекта: куб и сфера. Мы собираемся отобразить куб в точке с координатами (-3, 2, 6), а сферу в точке (5, 0, -2) мировой системы координат. Это можно проделать с помощью следующих шагов.
| C++ | D3DXMATRIX matCube, matSphere; D3DXMatrixTranslation(&matCube, -3.0f, 2.0f, 6.0f); pDirect3DDevice->SetTransform(D3DTS_WORLD, &matCube); drawCube(); D3DXMatrixTranslation(&matSphere, 5.0f, 0.0f, -2.0f); pDirect3DDevice->SetTransform(D3DTS_WORLD, &matSphere); drawShepre(); |
| Pascal | var matCube, matSphere: TD3DXMatrix; … D3DXMatrixTranslation(matCube, -3.0, 2.0, 6.0); device.SetTransform(D3DTS_WORLD, matCube); drawCube; D3DXMatrixTranslation(matShpere, 5.0, 0.0, -2.0); device.SetTransform(D3DTS_WORLD, matSphere); drawShepre; |
Построение проекции весьма сложная и очень неэффективная операция когда камера имеет произвольное положение и направление в мировой системе координат. Чтобы упростить эту ситуацию, мы перемещаем камеру в начало мировой системы координат и поворачиваем ее так, чтобы "взгляд" камеры был направлен в положительную сторону оси Z, как показано на рисунке ниже.
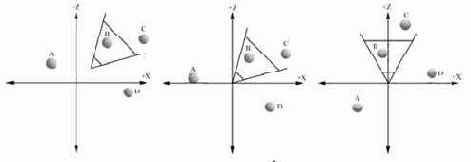
Матрица перехода в систему координат камеры может быть получена с помощью функции D3DXMatrixLookAtLH(), прототип которой показан ниже:
D3DXMatrixLookAtLH ( matView, // результат Eye, // положение камеры в мировой системе координат At, // точка в мировой системе, куда направлена камера (взгляд) Up // вектор, указывающий "где верх" в мировой системе координат ).
Для установки матрицы вида (преобразование в пространство камеры) используется метод SetTransform с первым параметром D3DTS_VIEW.
Например, поместить камеру в точку (0,0,-3) и направить "взгляд" наблюдателя в начало системы координат, можно с помощью такого кода:
| C++ | D3DXMATRIX matView; D3DXVECTOR3 positionCamera, targetPoint, worldUp; positionCamera = D3DXVECTOR3(0,0,-3); targetPoint = D3DXVECTOR3(0,0,0); worldUp = D3DXVECTOR3(0,1,0); D3DXMatrixLookAtLH(&matView, &positionCamera, &targetPoint, &worldUp); device->SetTransform(D3DTS_VIEW, &matView); |
| Pascal | var matView: TD3DMatrix; positionCamera, targetPoint, worldUp : TD3DXVector3; … positionCamera := D3DXVector3(0, 0, -3); targetPoint := D3DXVector3(0, 0, 0); worldUp := D3DXVector3(0, 1, 0); D3DXMatrixLookAtLH(matView, positionCamera, targetPoint, worldUp); device.SetTransform(D3DTS_VIEW, matView); |
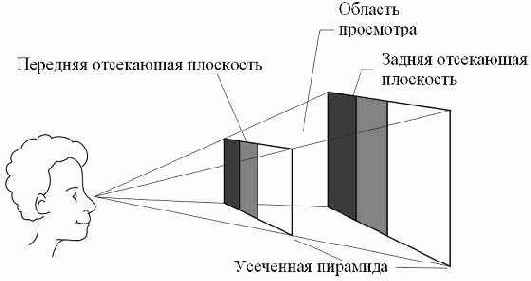
Последним этапом преобразования при получении 2D изображения является операция проекции. Библиотека поддерживает работу как с перспективной, так и с ортогональной проекциями.
Для работы с первым типом проекций предназначена функция D3DXMatrixPerspectiveFovLH(), для ортогональных же проекций нужна функция D3DXMatrixOrthoOffCenterLH(). Мы рассмотрим примеры работы с перспективной проекцией. Матрица перспективной проекции задает положение передней и задней отсекающих плоскостей, искажения, имитирующие перспективу. Прототип функции D3DXMatrixPerspectiveFovLH() приведен ниже.
D3DXMatrixPerspectiveFovLH( matProj, // результат fov, // вертикальный угол обзора aspect, // отношение ширины окна к высоте zn, // расстояние до передней отсекающей плоскости zf // расстояние до задней отсекающей плоскости )
Ниже приведены иллюстрации, которые поясняют значение последних четырех аргументов данной функции.
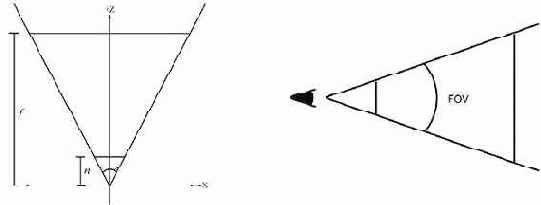
Для установки перспективной матрицы необходимо вызвать метод SetTransform с первым параметром D3DTS_PROJECTION. Приведенный ниже пример, создает и устанавливает матрицу проекции со следующими параметрами: вертикальный угол обзора – 45 градусов, расстояние до передней и задней отсекающих плоскостей – 1 и 100 единиц соответственно.
| C++ | D3DXMATRIX matProj; D3DXMatrixPerspectiveFovLH(&matProj, D3DX_PI/2, width/height, 1, 100); device->SetTransform(D3DTS_PROJECTION, &matProj); |
| Pascal | var matProj: TD3DXMatrix; D3DXMatrixPerspectiveFovLH(matProj, pi/2, Width/Height, 1, 100); device.SetTransform(D3DTS_PROJECTION, matProj); |
Таким образом, конвейер преобразований вершин объекта может быть описан следующей блок-схемой:
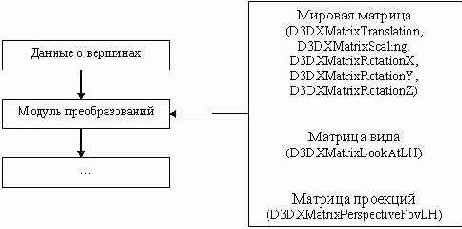
Каждая вершина трехмерной сцены подвергается следующему преобразованию V' = V*matWorld*matView*matProj, где V – исходная вершина, V' - преобразованная вершина.
