Расчет освещенности с помощью шейдеров

Рассмотрим теперь более подробно, как осуществляется расчет освещенности грани в библиотеке Direct3D. При закраске поверхностей объекта в идеале мы должны для каждой точки грани (полигона) вычислять интенсивность освещения методами, описанными выше. Во многих графических библиотеках, в том числе и в Direct3D прибегают к приближенным методам закраски граней трехмерного объекта, состоящего из полигонов в силу того, что процесс вычисления значения интенсивности для каждого пикселя, является вычислительно трудоемким. В компьютерной графике используют, как правило, три основных способа закраски полигональной сетки: однотонная закраска, закраска, основанная на интерполяции значений интенсивности, и закраска, построенная на основе интерполяции векторов нормали. Библиотека Direct3D располагает способами использования только двух первых методов.

При однотонной закраске вычисляется один уровень интенсивности, который используется для закраски всего полигона. При использовании закраски этого типа будет проявляться эффект резкого перепада интенсивности на всех граничных ребрах объекта.

Метод закраски, который основан на интерполяции интенсивности (метод Гуро), позволяет устранить дискретность изменения интенсивности. Процесс закраски по методу Гуро осуществляется следующими шагами:

определяется (вычисляется или изначально задается) нормаль к каждой вершине полигона; причем для различных полигонов, имеющих общую вершину, нормали, как правило, различаются;
вычисляются значения интенсивности в каждой вершине полигона, используя рассмотренные выше модели освещенности;
полигон закрашивается путем линейной интерполяции значений интенсивностей в вершинах сначала вдоль каждого ребра, а затем и между ребрами вдоль каждой сканирующей строки

В некоторых экзотических случаях и метод закраски Гуро не позволяет полностью устранить перепады интенсивности. В этом случае можно воспользоваться закраской по методу Фонга. Алгоритмически метод Фонга схож с методом Гуро. Но в отличие от интерполяции значений интенсивности в методе Гуро, в методе Фонга используется интерполяция векторов нормали вдоль сканирующей строки.
Функция mul() производит умножение вектора на матрицу, функция normalize() осуществляет нормировку вектора, функция dot() вычисляет скалярное произведение двух векторов. Как видно из представленных строк кода, для каждой вершины мы должны определять вектор на источник света и преобразовывать нормаль, как показано ниже.

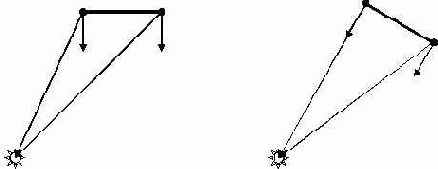
Таким образом, каждая вершина трехмерной модели получит цвет в соответствие с ее нормалью и вектором на источник. После выполнения этих шагов все вершины передаются на этап компоновки примитивов и растеризации. Растеризатор делит каждый треугольник на элементарные фрагменты (пиксели) и затем производит линейную интерполяцию текстурных координат и цвета.

Такой способ обработки дает возможность реализовать попиксельное освещение граней объекта. Реализовать это можно следующим образом. В силу того, что все атрибуты вершины (положение, цвет, текстурные координаты и т.д.), вычисленные в вершинном шейдере, интерполируются "по треугольнику", то можно, например, в качестве текстурных координат передать значения нормали вершины. Таким образом, графический конвейер воспримет нормаль как текстурные координаты вершины, и для каждого растеризуемого пикселя произведет интерполяцию векторов нормали. Входными данными для вершинного шейдера будут координаты вершины и нормаль.

struct VS_INPUT { float4 position : POSITION; float3 normal : NORMAL; };

Выходные данные вершинного шейдера мы описываем уже тройкой атрибутов: преобразованная вершина, преобразованная нормаль и вектор на источник света.

struct VS_OUTPUT { float4 position : POSITION; float3 light : TEXCOORD0; float3 normal : TEXCOORD1; };

Следует заметить, что атрибуты вершины нормаль и вектор на источник определены как текстурные координаты размерности 3 (float3). Тело вершинного шейдера будет выглядеть следующим образом.

VS_OUTPUT main_vs( VS_INPUT In ) { VS_OUTPUT Out; Out.position = mul( In.position, WorldViewProj ); float3 pos = mul( In.position, World ); Out.light = normalize(vecLight-pos); Out.normal = normalize(mul( In.normal, World )); return Out; }

Глобальные переменные будут такими же как и в предыдущем случае.

float4x4 WorldViewProj; float4x4 World; float4 vecLight;

Таким образом, пиксельный шейдер будет приминать на вход всего два вершинных атрибута: нормаль и вектор на источник. Сама же процедура пиксельного шейдера будет выглядеть так.

float4 main_ps(float3 light : TEXCOORD0, float3 normal : TEXCOORD1) : COLOR0 { float4 diffuse = {1.0f, 1.0f, 0.0f, 1.0f}; return diffuse*dot(light, normal); }

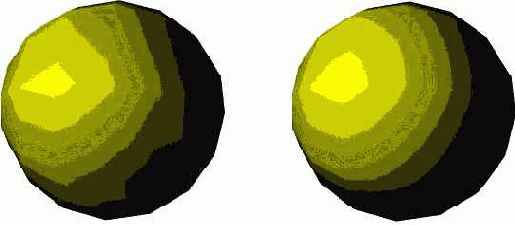
Ниже приведены примеры закраски по методу Гуро (слева) и Фонга (справа).

Рассмотрим еще один очень распространенный эффект построения реалистичных изображений, называемый bump-mapping или микрорельефное текстурирование, причем без существенных вычислительных затрат. Идея этого подхода заключается в моделировании рельефной поверхности с помощью двух текстур. Одна из них представляет собой изображение некоторой поверхности, а другая – так называемая карта нормалей. Карта нормалей представляет собой текстуру, где каждый пиксель является вектором нормали. Можно сказать, что карта нормалей несет в себе информацию о неровностях в каждом пикселе изображения. Как известно интенсивность освещения зависит от угла между нормалью в точке и вектором на источник света (закон косинусов Ламберта).

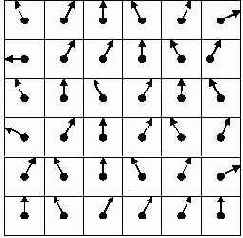
В зависимости от вектора нормали интенсивность в каждом пикселе будет различной. Следует заметить, что вектор нормали (nx, ny, nz) и цвет (R, G, B) кодируется тройкой чисел. Но цвет кодируется тремя положительными величинами из отрезка [0, 1], тогда как компоненты вектора нормали могут принимать и отрицательные значения. Так как координаты нормализованного вектора лежат в диапазоне [-1, 1], то можно с помощью линейного преобразования отобразить отрезок [-1, 1] в отрезок [0, 1]. Для этого можно воспользоваться следующей формулой: N*0.5+0.5, где N –вектор нормали. Такой процесс кодировки проделывается для каждого компонента вектора. Обратное преобразование (отрезок [0, 1] отобразить в отрезок [-1, 1]) может быть реализовано с помощью формулы 2*C–1, где C – значение цвета.

Например, вектор (1, 0, 1) будет преобразован в тройку чисел (1, 0.5, 1) – светло- фиолетовый цвет. Для получения карты нормалей из исходного изображения имеются специальные программы и алгоритмы, например, существует плагин к PhotoShop’у, с помощью которого можно получить карту нормалей. Ниже представлен пример текстуры и соответствующая ей карта нормалей.


Исходное изображение	Карта нормалей

Таким образом, для вычисления интенсивности в каждом пикселе необходимо:

Получить цвет из исходной текстуры;
Получить закодированное значение вектора нормали из карты нормалей;
Произвести преобразование значений из цветового пространства в пространство нормалей;
Вычислить скалярное произведение нормали на вектор источника света;
Умножить полученное значение на цвет исходной текстуры.

Пиксельный шейдер, реализующий данные шаги показан ниже.

float4 Light; sampler tex0; sampler tex1;

struct PS_INPUT { float2 uv0 : TEXCOORD0; float2 uv1 : TEXCOORD1; float4 color: COLOR0; };

float4 Main (PS_INPUT input): COLOR0 { float4 texel0 = tex2D(tex0, input.uv0); float4 texel1 = 2.0f*tex2D(tex1, input.uv1) - 1.0f; return texel0*dot(normalize(Light), texel1); };

Значение положения источника света передается в пиксельный шейдер через переменную Light. Ниже показаны примеры микротекстурирования при различных положениях источника света.


return texel0*dot(normalize(Light), texel1);

return input.colortexel0dot(normalize(Light), texel1);

Содержание раздела